九艺网,魔度映绘旗下专业游戏动画学习网站 › 门户 ›Engine› PBR › 查看内容

彻底看懂PBR/BRDF方程

2022-3-26 12:26klbuafjvb 655 0

实时渲染中的PBR方程是这样的

$L_o = \int_{\Omega}^{} f_rL_icos\theta_i d\omega_i = \int_{\Omega}^{} (k_d \frac{ c}{\pi} + k_s\frac{DFG}{4cos\theta_icos\theta_o})L_icos\theta_i d\omega_i\\$

但是很多教程中对这些项的含义解释的不够清楚, 我在学习中遇到许多困惑. 搜索资料后找到的答案, 这里分享给大家. 阅读前需要读者对PBR有简单的了解.

1. L的单位是什么?

这其实是一个很重要的问题, 如果没有弄清楚单位, 整个PBR方程会令人非常困惑.

其实从

$L$

这个字母就可以看出来,

$L$

的单位是辐亮度, 常用的各种单位如下表所示:

$\begin{array}[b] {|c|c|} \hline 名称 & 单位 & 符号 & 对应色度单位 & 色度单位 \\ \hline Radiant\ energy/辐射能 & 焦耳 Q & Q & Luminous\ energy/光能量 & talbot \\ \hline Radiant \ flux /辐通量 & 瓦特 W& \Phi & Luminous\ flux/光通量 & 流明 lm \\ \hline Intensity/辐强度 & W/sr & I & Luminous\ intensity / 光出射度 & 坎德拉 cd =lm/sr\\ \hline Irradiance/辐照度 & W / m^2 & E & Illuminance/发光强度 &勒克斯lx=lm/m^2 \\ \hline \hline Radiance/辐亮度 & W / (m^2 sr) & L & Luminance/光亮度 & 尼特 nit=lm/(m^2sr) \\ \hline \end{array}\\$

色度学单位和辐度学单位是一一对应的, 详细的分析和转换过程可以参考 https://zhuanlan.zhihu.com/p/118272193.

辐度学单位描述真实的物理辐射, 色度学单位描述人眼的感受. PBR方程使用两种单位系统都是可以的, 我们在这里使用辐度学单位.

需要注意的是辐亮度的定义为:

$L= \frac{d\Phi}{dwdA^\bot}=\frac{d\Phi}{dwdAcos\theta}\\$

这里下面除的面积是一个投影面积.

为什么要使用辐亮度这个单位呢? 我想原因主要是这两点:

(1) 符合光的传播特征, 光是发散式传播的, 辐亮度是一个不会随距离变化的量.

(2) 符合人眼的观察特征, 固定辐亮度的物体, 在任何距离观察亮度总是相同的.

这点是符合我们生活常识的. 原因的话可以理解为距离变远后, 虽然到达人眼的辐通量变少了, 但是形成的像也变小了, 所以看到的亮度不变.

这里用数学方式再来验证下:

设距离

$r_1$

处的一微元表面, 面积为

$dA$

, 辐射度为

$L$

, 人眼瞳孔面积为

$S$

, 视网膜到瞳孔距离为

$r_2$

微元表面在瞳孔上形成的立体角为

$d\omega = \frac{dA}{ \pi r_1^2}$

, 通过瞳孔的辐通量

$d\Phi = d\omega L S= \frac{dALS}{ \pi r_1^2}$

, 设微元表面在视网膜上成像大小为

$dA'$

, 已知

$\frac{r_1^2}{dA} = \frac{r_2^2}{dA'}$

, 得

$dA' = \frac{dAr_2^2}{r_1^2}$

. 微元表面在视网膜上成像产生的辐照度

$E = \frac{d\Phi}{dA'} = \frac{dALS}{ \pi r_1^2} \cdot \frac{r_1^2}{ dAr_2^2} = \frac{LS}{\pi r_2^2}$

所以

$E$

不会随着

$r_1$

的变化而变化, 在不同距离观察的亮度是相同的.

2. BRDF到底是啥?

首先不考虑BRDF函数, 我们来计算下整个半球面上的辐照度

$E$

$E(p) = \int_{\Omega}^{} L_i(p, \omega) cos\theta_i d\omega_i\\$

把整个辐照度看作是半球上的辐亮度积分,可得:

$dE(p, \omega_i) = L_i(p, \omega_i) cos \theta_i d\omega_i \\$

而在任意方向上出射的光的辐亮度微分和任意方向上入射光辐亮度微分成正比的:

$d L_o(p, \omega_o) \propto dE(p, \omega_i)\space \\$

这个比例就是关于

$\omega_i$

和

$\omega_o$

的BRDF函数, 记为:

$f_r(p, \omega_o, \omega_i) = \frac{d L_o(p, \omega_o)}{ dE(p, \omega_i)} = \frac{d L_o(p, \omega_o)}{ L_i(p, \omega_i) cos \theta_i d\omega_i } \space\\$

需要注意的是这两个微分的不同,

$dL_o$

是关于值的微分,

$dE$

是在立体角上的微分.

BRDF函数乘以辐照度值, 得到的是辐亮度, 使单位发生了变化.

这样在整个半球面上积分,得到:

$L_o(p, \omega_o) = \int_{\Omega}^{} f_r(p, \omega_i, \omega_o) L_i(p, \omega_i) cos \theta_i d\omega_i \space \\$

BRDF满足:

(1) 交换律:

$f_r(p, \omega_i, \omega_o) = f_r(p, \omega_o, \omega_i)$

(2) 能量守恒:

$\int_{\Omega}^{} f_r(p, \omega_o, \omega') cos \theta d\omega' \leq 1$

3. 菲涅尔反射的含义是什么? 金属和电介质的菲涅尔项有什么不同?

菲涅尔反射描述一个完全平坦的，由两个不同折射率介质组成的表面对光的反射率。

在不同折射率的介质相交表面，光会部分反射且部分折射，反射的比例就是菲涅尔系数。菲涅尔系数满足

$0 \leq F_r \leq 1$

。

菲涅尔系数是可以由麦克斯韦方程组直接推导出来的，形式也很复杂。

已知两种介质的折射率分别为

$\eta_i,\eta_t$

。首先根据斯涅尔定律得到折射角和入射角的关系：

$\eta_i sin\theta_i = \eta_t sin\theta_t\\$

然后根据麦克斯韦方程组计算推导，平行和垂直偏振光的菲涅尔反射公式：

$r_{||}= \frac{\eta_tcos\theta_i-\eta_icos\theta_t}{\eta_tcos\theta_i+\eta_icos\theta_t},\\ r_\bot= \frac{\eta_icos\theta_i-\eta_tcos\theta_t} {\eta_icos\theta_i+\eta_tcos\theta_t},$

渲染中我们无需考虑偏振光的影响，得到：

$F_r = \frac{1}{2}(r_{||}^2 + r_\bot^2)\\$

不同材质的菲涅尔系数做成图示例如下：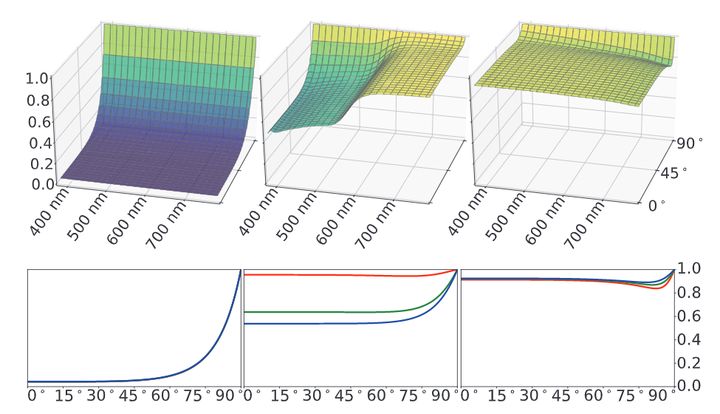

可以看出在观察角度接近掠夺角(90度)的时候，菲涅尔系数都是趋近于1的，这种现象叫做菲涅尔现象。

接下来要分开讨论电介质和金属：

A.电介质

可以看出，对于电介质来说，菲涅尔系数基本上不会随着波长变化。

我们现在用Schlick近似来表示菲涅尔系数：

将观察角为0时的菲涅尔系数记为

$F_0$

，将两种介质的折射率比例记为

$n$

，得

$F_0 = (\frac{n+1}{n-1})^2\\$

Schilick近似为：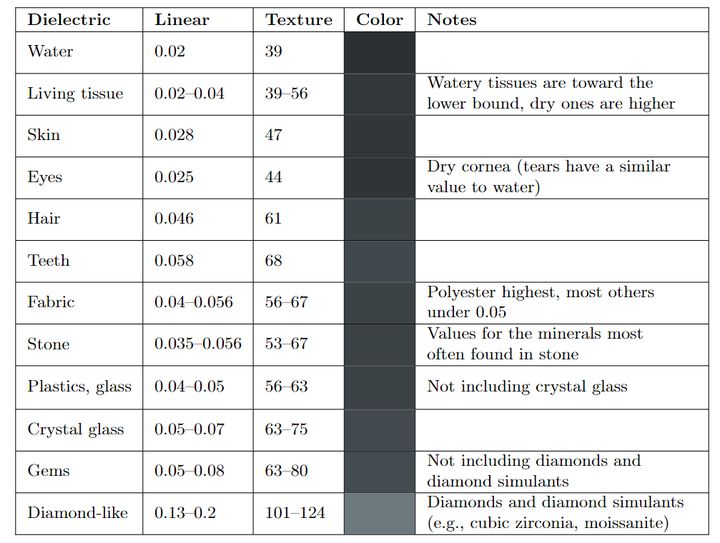

$F_r\approx F_0 + (1-F_0)(1-cos\theta_i)^5\\$

常见电介质的

$F_0$

值为：

可以看出电介质的

$F_0$

值一般都很小，在实时渲染中，我们直接取0.04作为默认值。

另外需要知道的是，我们这里的菲涅尔项是反射的比例，没有被反射的部分自然是形成折射。因为这里讨论的是不透明表面光，折射部分的光传入介质内部后，部分被吸收，部分再次出射形成漫反射/次表面散射。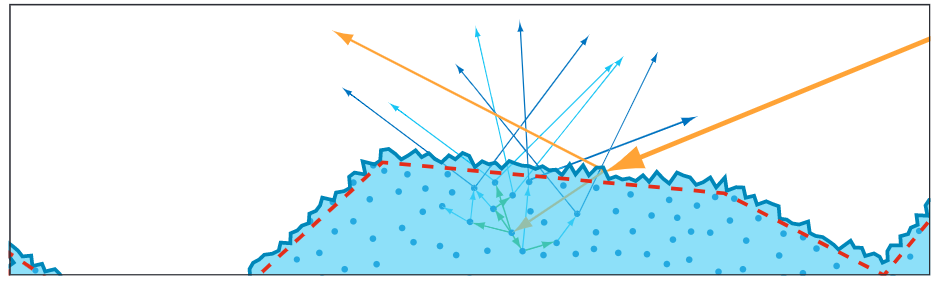

B.金属

金属和电介质的区别主要体现在这两点:

(1) 金属的折射率是复数, 金属的折射率表示为

$\bar{\eta} = \eta+ik$

$k$

表示吸收率.

这里菲涅尔公式仍然适用, 只是计算起来会复杂一点.

上面我们说电介质的菲涅尔表示反射比例, 剩余的部分是折射. 对于金属来说, 因为金属内部是可以自由运动的电子, 剩余的部分是直接被金属吸收了. 也就是说, 金属不会产生漫反射.

(2) 金属的折射率随光波长变化剧烈, 因此在Schilick近似时, 我们要把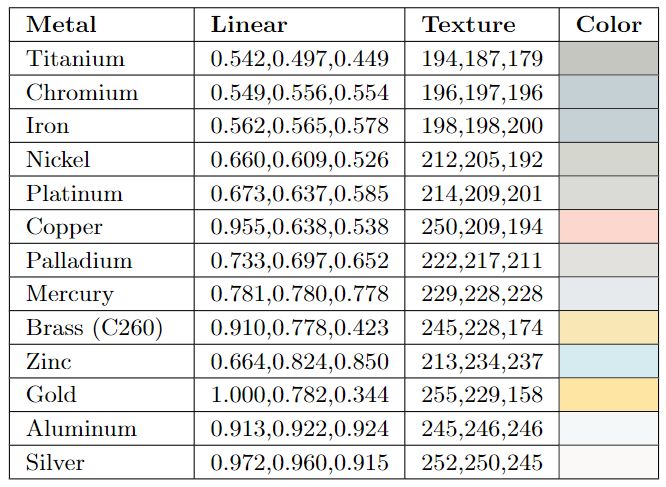

$F_0$

用RGB三个分量来表示, 常见金属的

$F_0$

值如下所示:

从这个性质也可以知道, 电介质的颜色是来自于漫反射, 而金属的颜色是来自于菲涅尔反射/镜面反射.

4. BRDF如何表示全镜面反射?

对于一个全镜面反射来说, 只需要考虑菲涅反射的系数, 也就是说

$L_o(\omega_o) = F_r(\omega_r)L_i(\omega_r) =\int_{\Omega}^{} f_r(\omega_o,\omega_i)L_i(\omega_i)cos\theta_id\omega_i\\$

这里

$\omega_r$

和

$\omega_o$

是关于表面法线对称的.

现在的问题是, 我们如何描述这里的

$f_r$

BRDF项? 答案是使用狄拉克

$\delta$

函数,

$\delta$

函数满足:

$\delta(x) = \begin{cases} \infty& {x=0}\\ {0}& {x\ne0} \end{cases}\\ \int_{-\infty}^{+\infty} \delta(x) = 1\\ \int_{-\infty}^{+\infty}f(x) \delta(x-x_0)dx = f(x_0)\\$

这样, 将狄拉克函数带入到方程中, 得到:

$L_o = \int_{\Omega}^{} \frac{ \delta(\omega_i-\omega_r)}{cos\theta_i} F_r(\omega_i)cos\theta_id\omega_i=F_r(\omega_r)L_i(\omega_r)\\$

得到BRDF的表示为:

$f_r(p, \omega_o, \omega_i) = F_r(\omega_r) \frac{ \delta(\omega_i-\omega_r)}{cos\theta_i} \\$

5. 如何理解漫反射?

前面我们已经讲过漫反射形成的原因, 就是没有被菲涅尔反射的部分, 再次出射形成的.

我们通常使用Labertian模型来描述漫反射, 这种模型假定在所有方向观察物体表面的亮度完全相同.

Lambertian模型下的BRDF函数表示为

$f_r = \frac{c }{\pi}$

$c$

叫做反照率或者固有色, 表示光在介质内部出射部分的比例,

$1-c$

表示被介质吸收的比例.

现在来解释下为什么这里要除以

$\pi$

, 这也是一个经常令人困惑的地方.

在Lambertian漫反射模型下 , 由能量守恒可知

$\int_{\Omega}^{} f_r(\omega_o, \omega') cos\theta d\omega' = c\space\\$

因为Lambertian漫反射假设在所有方向观察亮度都是相同的, 因此漫反射的BRDF

$f_r$

和

$\omega_i,\omega'$

是无关的, 是一个常数, 将

$f_r$

提到外面得:

$f_r\int_{\Omega}^{} cos\theta d\omega' = c\\ f_r\int_{\Omega}^{} cos\theta d\omega' = f_r \int_{0}^{2\pi}d\varphi \int_{0}^{\frac{\pi}{2}} \cos\theta \sin \theta d\theta =f_r\pi=c\\ f_r = \frac{c}{\pi}$

我们前面说过, BRDF的作用之一是将辐照度值

$E$

转换为辐亮度值

$L$

. 这里的

$\frac{1}{\pi}$

也可以看作是一个用来实现转换的系数.

在现实生活中的漫反射并不是完全符合Labertian漫反射模型的, Oren–Nayar漫反射模型等一些更加复杂的模型可以更好地表示现实中的漫反射.

但是在实际渲染中发现, 使用更加复杂的模型的提升很小. 出于性能考虑, 目前在实时渲染中Lambertian模型还是主流.

6. 如何理解微表面模型在镜面反射中的应用?

微表面模型在BRDF中体现在法线分布项D和几何遮蔽项G.这里我们来分别分析下.

前面我们讲到菲涅尔反射的比例, 都是针对完全镜面反射, 即

$\omega_i$

和

$\omega_o$

关于表面法线对称.

在微表面模型中, 只有微元表面法线朝向

$\omega_h = \frac{\omega_i+\omega_o}{2}$

(这种写法不严格, 明白其含义即可)的时候, 我们才能看到物体表面的某个微元, 法线分布函数

$D(\omega_h)$

, 就是一个描述

$\omega_h$

分布方向的概率密度函数.

对于完全光滑的平面,

$D(\omega_h) = \delta(\omega_h - (0, 0, 1))$

对于粗糙的平面, 我们使用参数

$\alpha$

来表示表面粗糙程度, 并使用函数来近似.

从物理合理的角度来说, 法线分布函数必须满足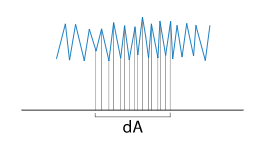

$\int_{H^2(n)}^{} D(\omega_h)cos\theta_hd\omega_h = 1$

. 也就是说, 在一小块面积为

$dA$

的表面上, 各个法线方向的面积的投影和还是

$dA$

从BRDF单位转换的角度来说, D项是负责将辐照度值

$E$

转换为辐亮度值

$L$

的部分, 类似于漫反射中的

$\frac{1}{\pi}$

几何分布函数有很多种近似模型, 常用的一个为Trowbridge-Reitz GGX:

$D(\omega_h) = \frac{\alpha ^2}{\pi (cos\theta_h^2(\alpha^2-1)+1)^2}.\\$

既然微表面模型假设微表面是崎岖不平的, 自然会产生遮挡, 导致某些部分我们无法看到. 定义遮挡函数

$G_1(\omega, \omega_h)$

, 表示微表面法线为

$\omega_h$

时, 我们从

$\omega$

方向观察时, 能看到的物体表面的比例. 遮挡函数满足

$0 \leq G_1(\omega, \omega_h) \leq1$

对于一般的表面来说, 微表面可见的比例和法线

$\omega_h$

是无关的, 因此我们直接省略

$\omega_h$

, 将遮挡函数记为

$G_1(\omega)$

从物理合理的角度来说, 一块面积为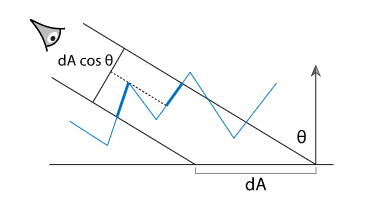

$dA$

的微表面, 从

$\omega$

方向观察时, 能观察到的面积之和必然是

$dA cos\theta$

. 因此遮挡函数必须满足

$cos\theta = \int_{H ^2(n)} G_1(\omega, \omega_h) max(0, \omega \cdot \omega_h)D(\omega_h)d\omega_h.\\$

因为光在入射到平面上时也会有遮挡, 所以可以得到几何衰减项为:

$G(\omega_o, \omega_i) = G_1(\omega_o)G_1(\omega_i).\\$

一个常用的几何衰减的近似为Schlick-GGX近似:

$G_1(\omega) = \frac{cos\theta}{cos\theta(1-k)+k}, k = \begin{cases} \frac{(\alpha+1)^2}{8}& {直接光照}\\ {\frac{\alpha^2}{2}}& {IBL} \end{cases}\\ G(\omega_o, \omega_i) = G_1(\omega_o)G_1(\omega_i)$

7. 镜面反射的BRDF如何推导?

现在我们已经有了Torrance–Sparrow模型下镜面反射BRDF需要的DFG各项函数, 来推导下BRDF镜面反射的表示. 很多PBR教程这步都是直接给出一个结论, 没有具体的推导过程.

微表面模型中, 每个微表面都是产生完全镜面反射. 现在考虑从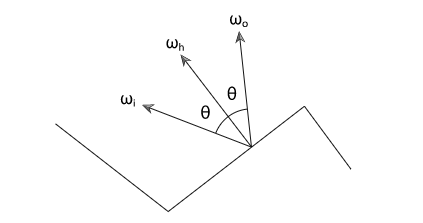

$\omega_i$

方向入射的光线, 从

$\omega_o$

方向观察, 只有微元表面法线朝向

$\omega_h = \frac{\omega_i+\omega_o}{2}$

的时候才产生反射.

我们在这里定义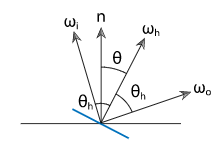

$\theta_h$

为

$\omega_h$

和

$\omega_i$

之间的夹角(在前面我们的

$\theta_h$

表示的是和表面法线之间的夹角).

先不考虑几何衰减项

$G$

, 在一个面积为

$dA$

的微表面上, 可以看到的反射部分面积为

$dA(\omega_h) = D(\omega_h)d\omega_hdA\\$

入射光辐亮度为

$L_i$

, 由辐亮度定义可知, 入射到

$dA(\omega_h)$

上的辐照度为

$d\Phi_h = L_i(\omega_i)d\omega_i dA(\omega_h)=L_i(\omega_i)d\omega_i D(\omega_h)d\omega_hdAcos\theta_h\\$

根据菲涅尔定理, 且我们这里不考虑几何遮挡, 得到出射辐照度和入射辐照度满足:

$d\Phi_o = F_r(\omega_o)d\Phi_h\\$

再次由辐亮度定义得到出射的辐亮度满足:

$L(\omega_o)=\frac{d\Phi_o}{d\omega_ocos\theta_odA} = \frac{F_r(\omega_o) L_i(\omega_i)d\omega_i D(\omega_h)d\omega_hdAcos\theta_h}{d\omega_ocos\theta_odA} \\$

现在来计算

$\frac{d\omega_h}{d\omega_o}$

,这里以

$\omega_i$

作为为球坐标系向上的方向, 得

$\frac{d\omega_h}{d\omega_o} = \frac{sin\theta_h'd\theta_h'd\phi_h'}{sin\theta_o'd\theta_o'd\phi_o'}\\$

$\theta_h'$

表示

$\omega_h, \omega_i$

之间的夹角, 和上面

$\theta_h$

的定义是相同的,

$\theta_h'= \theta_h$

这里的

$\theta_o'$

表示

$\omega_o, \omega_i$

之间的夹角, 因为

$\omega_i, \omega_o$

关于

$\omega_h$

对称, 得

$\theta_o' = 2\theta_h'=2\theta_h$

,且

$\phi_o'=\phi_h'$

.得

$\frac{d\omega_h}{d\omega_o} = \frac{sin\theta_hd\theta_hd\phi_h}{sin(2\theta_h)2d\theta_hd\phi_h} =\frac{sin\theta_h}{4cos\theta_hsin\theta_h} =\frac{1}{4cos\theta_h}\\$

带入后化简得:

$L(\omega_o) = \frac{F_r(\omega_o) L_i(\omega_i) D(\omega_h)d\omega_i}{4cos\theta_o}\\$

再把几何衰减项带入得到完整的Torrance–Sparrow BRDF:

$f_r(\omega_o, \omega_i) = \frac{F_r(\omega_o) D(\omega_h)G(\omega_o, \omega_i)}{4cos\theta_ocos\theta_i}\\$

8. 实时渲染中整个渲染方程如何确定?

现在就是确定整个的PBR方程.由前面的计算可以得到PBR方程为:

$L_o = \int_{\Omega}^{} f_rL_icos\theta_i d\omega_i = \int_{\Omega}^{} (k_d \frac{ c}{\pi} + k_s\frac{DFG}{4cos\theta_icos\theta_o})L_icos\theta_i d\omega_i\\$